Формирующий эксперимент

Формирующий эксперимент осуществлялся в течение месяца в виде проведения цикла из 10 коррекционно-развивающих занятий, целью которых было развитие логического мышления у детей младшего школьного возраста с помощью игр. Занятия проводились со всей группой детей в форме дополнительной кружковой работы, часть заданий выполнялась детьми на основных уроках математики, или выполнялось ими как домашнее задание (краткие конспекты системы коррекционно-развивающих занятий с детьми - приложение №2).

Поскольку констатирующий эксперимент показал, что наибольшие затруднения дети используют в заданиях, требующих высокого уровня развития анализа и синтеза, которые являются важнейшими мыслительными операциями, нами было обращено большое внимание на развитие именно этих процессов. Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез - это соединение различных элементов, сторон объекта в единое целое.

В мыслительной деятельности человека анализ и синтез дополняют друг друга, так как анализ осуществляется через синтез, синтез - через анализ. Способность к аналитико-синтетической деятельности находит свое выражение не только в умении выделять элементы того или иного объекта, его различные признаки или соединять элементы в единое целое, но и в умении включать их в новые связи, увидеть их новые функции.

Формированию этих умений может способствовать: а) рассмотрение данного объекта с точки зрения различных понятий; б) постановка различных заданий к данному математическому объекту.

Для рассмотрения данного объекта с точки зрения различных понятий предлагались задания на классификацию или на выявление различных закономерностей (правил). Например:

По каким признакам можно разложить пуговицы в две коробки?

Особую роль в организации продуктивной деятельности младших школьников в процессе обучения математике играет прием сравнения. Формирование умения пользоваться этим приемом осуществлялось поэтапно, в тесной связи с изучением конкретного содержания. При этом мы ориентировались на такие этапы этой работы:

выделение признаков или свойств одного объекта;

установление сходства и различия между признаками двух объектов;

выявление сходства между признаками трех, четырех и более объектов.

В качестве объектов сначала использовались предметы или рисунки с изображением предметов, хорошо знакомых детям, в которых они могут выделить те или иные признаки, опираясь на имеющиеся у них представления.

Для организации деятельности учащихся, направленной на выделение признаков того или иного объекта, предлагался такой вопрос:

Что вы можете рассказать о предмете? (Яблоко круглое, большое, красное; тыква - желтая, большая, с полосками, с хвостиком; круг - большой, зеленый; квадрат - маленький, желтый).

В процессе работы закреплялись понятия "размер", "форма" и предлагались следующие вопросы:

Что вы можете сказать о размерах (формах) этих предметов? (Большой, маленький, круглый, как треугольник, как квадрат и т.д.)

Для выявления признаков или свойств какого-то предмета обычно обращались к детям с вопросами:

В чем сходство и различие этих предметов? - Что изменилось?

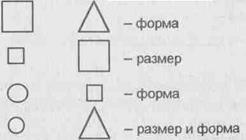
Дети уже знакомы с термином "признак" и он использовался при выполнении заданий: "Назови признаки предмета", "Назови сходные и различные признаки предметов".

Задания, связанные с приемом классификации, обычно формулировались в таком виде: "Разбейте (разложите) все круги на две группы по какому-то признаку". Большинство детей успешно справляются с этим заданием, ориентируясь на такие признаки, как цвет и размер. По мере изучения различных понятий задания на классификацию включали числа, выражения, равенства, уравнения, геометрические фигуры. Например, при изучении нумерации чисел в пределах 100 детям предлагалось такое задание:

Разбейте данные числа на две группы, чтобы в каждой оказались похожие числа:

а) 33, 84, 75, 22, 13, 11, 44, 53 (в одну группу входят числа, записанные двумя одинаковыми цифрами, в другую - различными);

б) 91, 81, 82, 95, 87, 94, 85 (основание классификации - число десятков, в одной группе чисел оно равно 8, в другой - 9);

в) 45, 36, 25, 52, 54, 61, 16, 63, 43, 27, 72, 34 (основание классификации - сумма "цифр", которыми записаны данные числа, в одной группе она равна 9, в другой - 7).

Таким образом, при обучении математике использовались задания на классификацию различных видов:

1. Подготовительные задания. К ним относятся: "Убери (назови)"лишний" предмет", "Нарисуй предметы такого же цвета (формы, размера)", "Дай название группе предметов". Сюда же можно отнести задания на развитие внимания и наблюдательности: "Какой предмет убрали?" и "Что изменилось?".

Возрастные особенности учеников младшего школьного возраста
Младшим школьным возрастом считается возраст детей примерно от 6-7 до 10-11 лет, что свидетельствует годам обучения в начальных классах общеобразовательной школы. В.А. Крутецкий определяет границы младшего школьного возраста с 7 до 11 лет, это соответствует годам обучения в начальных классах общеоб ...

Мотивация – движущая сила в учении
Мотив (от лат. moveo – двигаю) – общее название для процессов, методов, средств побуждения учащегося к продуктивной познавательной деятельности, активному освоению содержания образования. Случайно ли мотивация учения, учебному труду, познавательной деятельности, предмету, занимающего ведущие места ...

Возрастная и педагогическая психология
Эти две прикладные отрасли психологии, если их рассматривать вместе как единую учебную дисциплину, представляет собой применение общепсихологической теории для объяснения возрастного развития в детские годы (это наиболее исследованный отрезок жизни человека) и психологических условий эффективности ...