Планы-конспекты уроков по оптике для 11 класса

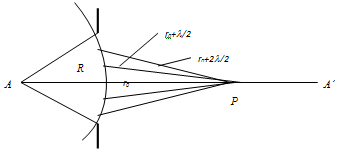
Амплитуда колебаний, обусловленных в точке Р отдельной зоной, зависит от площади зоны, от расстояния r от зоны до точки Р и от угла между отрезком r и нормалью к поверхности зоны. Площади зон примерно одинаковы и равны, 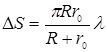, где R – радиус кривизны волнового фронта в створе отверстия, r0 – расстояние от отверстия до точки наблюдения P. Амплитуды волн, доходящих до точки наблюдения Р, зависят только от расстояния rk и от угла, составленного направлением этого отрезка с нормалью к поверхности зоны. С увеличением номера зоны расстояние rk и угол наклона возрастают, поэтому амплитуды колебаний, обусловленных в точке Р отдельными зонами, должны монотонно убывать с ростом номера зоны:

.

Так как фазы колебаний, обусловленных в точке Р соседними зонами, противоположны, то амплитуда Ak суммарного колебания, обусловленного действием k зон, равна

,

где знак последнего слагаемого положителен при нечетном k и отрицателен при четном k. При нечетном числе зон амплитуда результирующего колебания больше, чем при четном числе зон, укладывающихся в отверстии.

Учитывая монотонность убывания с ростом номера зоны амплитуды колебаний, обусловленных отдельными зонами, можно доказать приближенное равенство

,

где знак "+" соответствует нечетному числу зон, а знак "−" − четному числу зон.

Если между точечным источником и точкой наблюдения нет никаких препятствий, то есть фронт волн, распространяющихся от источника, полностью открыт, то и интенсивность света в точке наблюдения обусловлена только центральной зоной Френеля, то есть свет распространяется в эту точку прямолинейно.

Одновременно Френелем был проведен также количественный расчет распределения интенсивности при дифракции света на различных рода препятствиях.

Любопытный случай произошел на заседании Французской академии наук в 1818 г. Один из ученых, присутствовавших на заседании, – Пуассон обратил внимание на то, что из теории Френеля вытекают факты, явно противоречащие здравому смыслу. Из полученных Френелем формул следовало, что при определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре дифракционной картины должно находиться темное пятнышко, а за маленьким непрозрачным диском, наоборот, в центре тени должно находиться светлое пятно. Каково же было удивление ученых, когда эти факты были экспериментально доказаны в опытах Френеля и Араго.

Из-за того что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции нужно либо использовать очень маленькие препятствия, или же располагать экран далеко от препятствий. При расстоянии между препятствием и экраном порядка метра размеры препятствий не должны превышать сотых долей миллиметра. Если же расстояние до экрана достигает сотен метров или нескольких километров, то дифракцию можно наблюдать на препятствиях размером в несколько сантиметров и даже метров.

Психолого-педагогические проблемы развития сюжетной игры у дошкольников
Проблемы игры как формы организации жизни и деятельности детей постоянно находятся в центре внимания педагогов и психологов. Большинство отечественных ученых объясняют игру как особый вид деятельности, сложившийся на определенном этапе развития общества. Г.В. Плеханов, изучая проблему происхождения ...

Особенности работы социального педагога
Деятельность социального педагога с семьей включает три основных составляющих социально-педагогической помощи: образовательную, психологическую, посредническую. Рассмотрим последовательно каждую из составляющих. Образовательная составляющая включает в себя два направления деятельности социального п ...

Условия развития сюжетных игр детей среднего дошкольного возраста в дошкольном учреждении
Задачи: - Выявить уровень развития сюжетной игры у детей средней группы. - Проанализировать состояние предметно-игровой среды в средней группе детского сада. - Выявить особенности руководства воспитателями сюжетными играми детей. - Выявить особенности методической работы по организации руководства ...